中学生でもわかる地震の震源 距離 求め方：計算公式と防災の知識

地震が起きたとき、自宅が震源地からの距離の求め方のどこにあるのか、どのようにして震源の深さ 求め方を知るのか、疑問に感じたことはありませんか。特に中1 理科 地震 震源からの距離 求め方を習ったものの、実際の震源 距離 求め方を忘れてしまった方も多いかもしれません。

この記事では、地震発生時刻 求め方や震源からの距離 求め方 公式、そして震源からの距離 計算式といった地震の計算の基本を、震源までの距離 解き方 求め方の知識に焦点を当てて、防災士の視点から、理科が苦手な方でもわかりやすく解説していきます。この知識は、学校のテスト対策だけでなく、いざという時の冷静な行動にもつながります。ぜひ最後までお読みください。

この記事を読むと、次のことがわかります

• P波とS波の違いと、初期微動継続時間の意味が理解できる
• 震源までの距離を求める公式と計算式がわかる
• 複雑なデータから地震発生時刻や震源の深さを計算できるようになる
• 地震の計算問題でよくある間違いと、その対策を知ることができる

地震の計算は一見難しそうですが、使う公式は速さ・時間・距離の関係だけです。一つずつ丁寧に解説しますので、一緒にマスターしていきましょう！

防災視点から学ぶ地震の震源 距離 求め方

• 地震波（P波とS波）の基本をわかりやすく解説
• 中1 理科 地震 震源からの距離 求め方の全体像
• 初期微動継続時間を用いた震源までの距離　解き方　求め方
• 比例の考え方で導く震源からの距離 求め方 公式
• 観測データに基づく震源地からの距離の求め方について掘り下げる
• 正確な観測に必要な地震発生時刻　求め方
• 震源の深さ 求め方（三平方の定理の利用）

地震波（P波とS波）の基本をわかりやすく解説

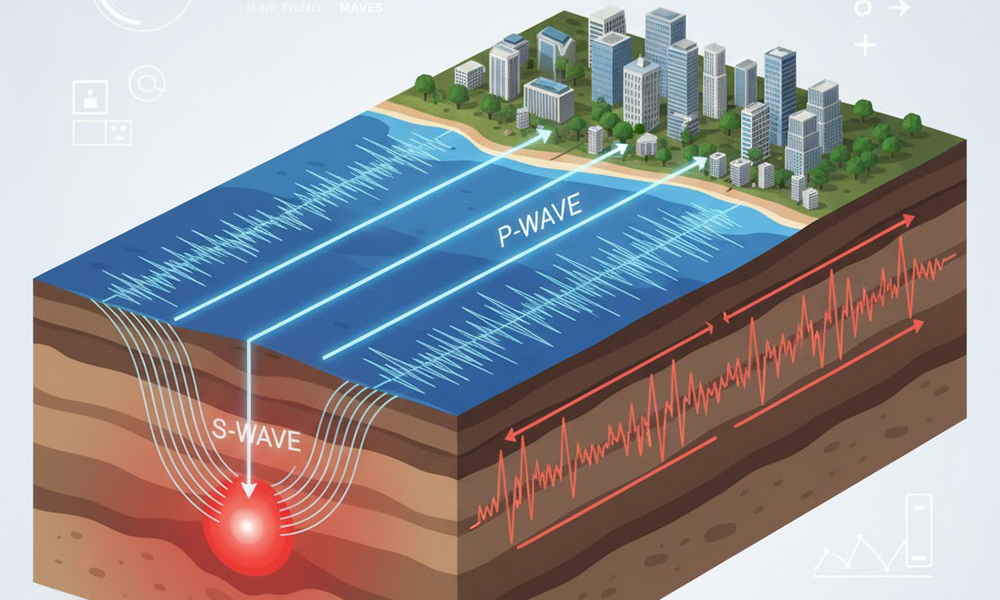
地震の震源距離を求める上で、最も基礎となるのがP波とS波という2種類の地震波の理解です。P波とS波は、それぞれ異なる速度で伝わり、異なる揺れ方をするのが特徴です。

特徴	P波（Primary Wave: 第一波）	S波（Secondary Wave: 第二波）
速度	速い（秒速5～7km程度）	遅い（秒速3～4km程度）
揺れ方	縦揺れ（進行方向と同じ向きに振動）	横揺れ（進行方向と垂直に振動）
感覚	最初にくる小さな「ドンッ」という揺れ（初期微動）	後にくる大きな「グラグラ」という揺れ（主要動）

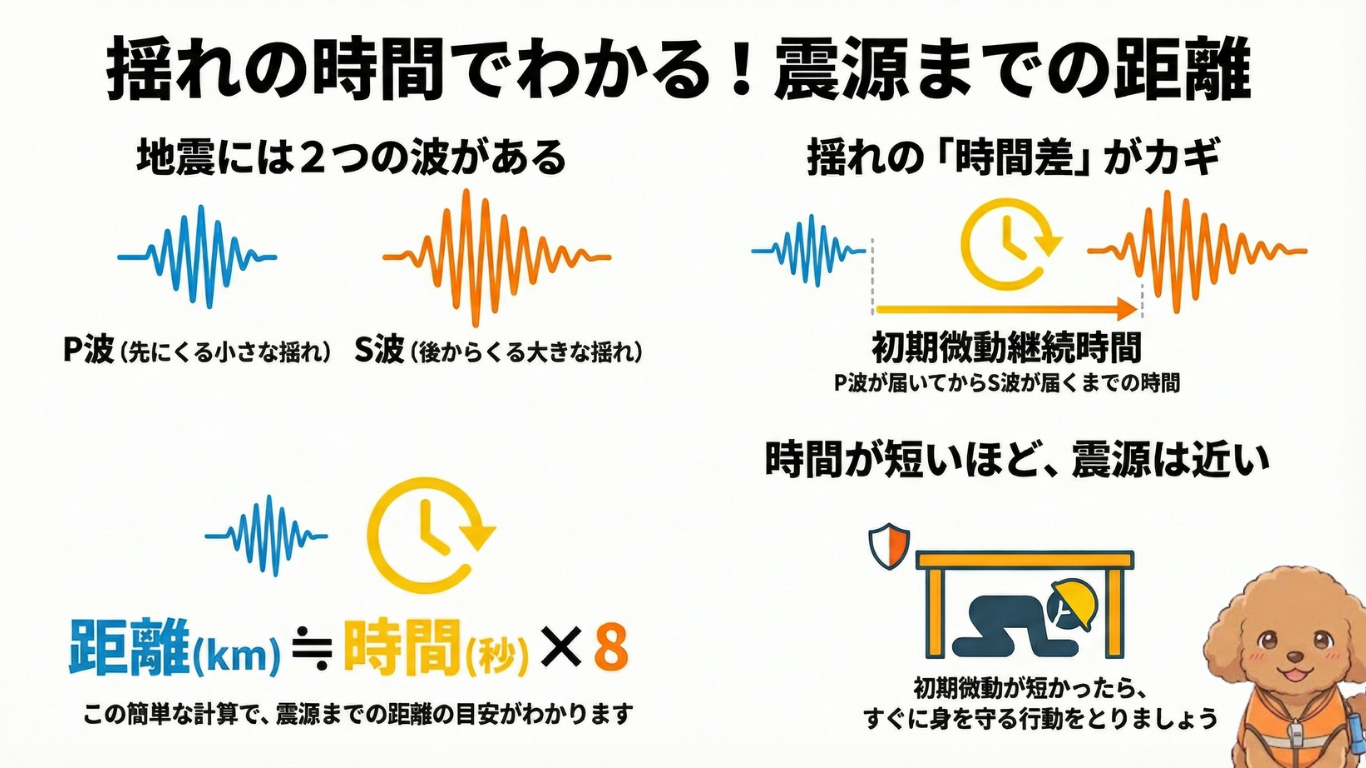
これらの波が観測地点に到達する時間の差を利用することが、震源までの距離を計算する鍵となります。P波が到着してからS波が到着するまでの時間を「初期微動継続時間」と呼びます。この継続時間が長ければ長いほど、観測地点は震源から遠いことになります。

P波は空気や水、固体など全ての物質を伝わりますが、S波は固体の中しか伝わることができません。この違いも、波の速度差につながる重要な要素です。

中1 理科 地震 震源からの距離 求め方の全体像

中学生の理科では、地震の計算問題を通じて、震源からの距離と**初期微動継続時間**が比例の関係にあることを学びます。これは、P波とS波の速度がほぼ一定であるため、観測地点が震源から離れるほど、速いP波と遅いS波の到達時間差（初期微動継続時間）が大きくなるためです。

震源からの距離を求める全体の流れは、主に二つのステップで構成されます。まず、複数の観測地点のデータを使ってP波とS波の速度を正確に求めます。次に、その求めた速度と、ある観測地点でのP波・S波の到着時刻の差（初期微動継続時間）を利用して、震源までの距離を算出するという流れです。

このように、単純な「速さ＝距離÷時間」の計算だけでなく、P波とS波の速度の差という、地震特有の物理現象を応用しているのがこの計算の面白いところです。

初期微動継続時間を用いた震源までの距離　解き方　求め方

初期微動継続時間を用いて震源までの距離を計算する方法は、地震学の基本となる重要な解き方です。この方法の根拠は、P波とS波の速度差にあります。P波が観測地点に到達した時刻からS波が到達した時刻を引くことで、初期微動継続時間がわかります。

震源距離（L）は、初期微動継続時間（t）、P波の速度（$V_p$）、S波の速度（$V_s$）を用いて、次の複雑な計算式で厳密に導かれます。

L = t × (Vp × Vs) / (Vp – Vs)

しかし、中学生の理科ではこの厳密な式は使わず、P波とS波の速度差から生じる「見かけの速さ」を約8km/sとして、非常にシンプルな経験則が使われることが多いです。前述の通り、この経験則は、平均的な地盤での波の速度に基づいたものです。

簡易的な震源距離の求め方（目安）

震源距離（km） ≒ 初期微動継続時間（秒） × 8

この簡易な方法でも、震源距離を推定できることを覚えておくと、地震発生時に役立つ知識になります。

比例の考え方で導く震源からの距離 求め方 公式

震源からの距離が初期微動継続時間に比例するという関係を利用すると、**比例式**を用いて未知の震源距離を簡単に求めることができます。この考え方は、2点間のデータが判明している場合に非常に有効です。

つまり、「震源からの距離」と「初期微動継続時間」の比は、どの観測地点でも一定になるという性質を使うのです。

比例式を使った求め方の手順

例えば、観測地点A（距離 $L_A$、継続時間 $t_A$）と、観測地点B（距離 $L_B$、継続時間 $t_B$）の2つのデータがわかっていると仮定します。

• もし $L_B$ が不明な場合は、比例式「$L_A : t_A = L_B : t_B$」を立てます。
• この比例式を解くと、「$L_A \times t_B = L_B \times t_A$」となるため、$L_B = (L_A \times t_B) \div t_A$ で震源からの距離 求め方 公式を求めることができます。

このように、比例式を使えば、P波とS波の正確な速度を知らなくても、震源までの距離を求めることができるのです。これは、地震の計算問題を解く際の大きな武器になりますね。

観測データに基づく震源地からの距離の求め方について掘り下げる

震源地からの距離の求め方について掘り下げるには、単一の観測地点からの計算だけでなく、複数の観測地点のデータを用いた三角測量の概念も知っておく必要があります。実際の地震観測では、初期微動継続時間から求めた各地点の震源距離を基に、より正確な震源位置を特定するのです。

まず、各観測地点から計算された震源距離を半径として、震源の位置を中心とする円を描きます。理論上、この円は3つの観測地点（A、B、C）から描かれた際に、一点で交わります。この交点こそが、地震の震源（震央）となるのです。

しかし、実際の観測では、地下の構造や地震計の設置誤差などにより、3つの円が完全に一点で交わることは稀です。そのため、多数の観測データを用いて、最も誤差が少なく、円が集中する場所を震源として特定するという、より複雑な解析が行われています。このように、地震観測は一つ一つの計算式だけでなく、総合的なデータ解析によって成り立っているのです。

正確な観測に必要な地震発生時刻　求め方

正確な震源距離を求めるためには、地震が実際に起きた正確な地震発生時刻を知ることが欠かせません。地震発生時刻 求め方は、P波の速度と観測地点でのP波到達時刻から、到達にかかった時間を逆算することで計算できます。

地震発生時刻の計算式

地震発生時刻 ＝ P波到達時刻 – P波が震源から到達するまでにかかった時間

P波が震源から到達するまでにかかった時間は、「震源からの距離 ÷ P波の速度」で求めることができます。例えば、P波の速度が8km/sで、震源からの距離が40kmの地点でP波が10時00分10秒に到達したとします。到達にかかった時間は 40km ÷ 8km/s = 5秒です。したがって、地震発生時刻は 10時00分10秒 – 5秒 = 10時00分05秒とわかります。

しかし、この計算を行うためには、事前に**P波の正確な速度**と**震源からの正確な距離**が分かっている必要があります。多くの問題では、この発生時刻を問われる前に、P波の速度を導出するステップが設けられています。

震源の深さ 求め方（三平方の定理の利用）

地震の揺れを議論する際、「震央」と「震源」という2つの場所を区別します。震央は、震源の真上にある地表の地点です。そして、観測地点と震央の間の距離を**震央距離**、観測地点と震源の間の距離を**震源距離**と呼びます。

震源の深さ 求め方は、この震央距離（D）、震源からの距離（R）、そして震源の深さ（H）の三つの値が、**三平方の定理**（ピタゴラスの定理）によって結びついていることを利用します。震源、震央、観測地点を結ぶと直角三角形ができるのです。

三平方の定理を用いた震源の深さの計算式

震源距離$^2$ ＝ 震央距離$^2$ ＋ 震源の深さ$^2$

R$^2$ = D$^2$ + H$^2$

したがって、H = $\sqrt{R^2 – D^2}$

前述の通り、この計算をするためには、まず初期微動継続時間から震源距離Rを正確に求める必要があります。このように、震源の深さは地震波の伝わり方と数学の知識を組み合わせて計算されているのです。

具体的な計算例と震源 距離 求め方の練習

• 観測データからP波とS波の速度を導出する
• P波とS波の速さを求める震源からの距離 計算式
• 間違いやすいポイントと計算ミスの対策
• 震源 距離 求め方をマスターして防災意識を高める

観測データからP波とS波の速度を導出する

地震の計算問題において、P波やS波の速度が最初から与えられていることはほとんどありません。多くは、2つの観測地点（A地点とB地点など）のデータから、まずこれらの**波の速度**を導出する必要があります。この導出には、速さの基本公式である「速さ ＝ 距離 ÷ 時間」を応用します。

ここで使う「距離」と「時間」は、震源からの距離そのものではなく、2地点間の「距離の差」と「到達時間の差」である点に注意が必要です。なぜなら、2地点の差を取ることで、不明である地震発生時刻の影響を打ち消すことができるからです。

速度導出の手順（P波の場合）

1. 距離の差を求める: （B地点の震源距離）-（A地点の震源距離）

2. 時間の差を求める: （B地点のP波到達時刻）-（A地点のP波到達時刻）

3. 速度を計算する: P波の速度 ＝ 距離の差 ÷ 時間の差

S波の速度も同様に、主要動の開始時刻の差を使って計算できます。この計算は、P波とS波が一定の速さで伝わっているという前提に基づいています。

P波とS波の速さを求める震源からの距離 計算式

前述の通り、P波とS波の速さを求める計算式は、2地点間のデータを使うのが基本ですが、一度波の速度が分かれば、震源からの距離を求める計算式は非常にシンプルになります。これは、観測地点に波が到達するまでにかかった時間を算出し、それに速さを掛けるという、速さの基本公式そのものです。

求めるもの	計算式（公式）	説明
P波が到達するまでの時間	P波到達時刻 – 地震発生時刻	P波の速度計算の準備
震源からの距離	P波の速度 × P波到達までの時間	距離を求める基本の計算式
震源からの距離	初期微動継続時間 × 見かけの速さ（約8km/s）	初期微動継続時間を使った簡易計算

これらの計算式を使いこなすことが、地震の計算問題、特に震源からの距離 計算式を正確に適用する上で非常に重要です。正確な速度が分かれば、未知の観測地点における震源距離も、この公式で導き出せます。

間違いやすいポイントと計算ミスの対策

地震の計算問題は、理科というよりはむしろ算数・数学の要素が強いため、計算ミスや概念の混同がよく発生します。ここでは、特に間違いやすいポイントと、それを防ぐための対策をまとめて解説します。

時刻と時間の混同

時刻（例：10時20分30秒）と時間（例：30秒間）の区別が曖昧になることがよくあります。「地震発生時刻 求め方」では時刻を、「初期微動継続時間」では時間を求めるため、何を計算しているのかを常に意識することが必要です。

対策: 問題文で「時刻」を問われているのか、「時間」を問われているのかを、問題用紙に丸を付けるなどして確認しましょう。計算結果が秒数なのに「〇時〇分〇秒」と書かないように注意が必要です。

単位変換のミス

速度の単位（km/sとm/s）や時間の単位（分と秒）が混在することもミスのもとです。例えば、震源からの距離がkmで、P波の速度をm/sで計算しようとすると、答えが大きくずれてしまいます。

対策: 計算を始める前に、全ての単位を統一してください。通常、地震の計算では「km」と「秒」に統一することが多いですが、問題の指示に従い、分速や時速の場合は全て秒速に、mの場合は全てkmに変換しましょう。

例: 1分 ＝ 60秒、1km ＝ 1000m

震源 距離 求め方をマスターして防災意識を高める

ここまで、P波とS波の違いから、初期微動継続時間を用いた震源までの距離 解き方 求め方、そして震源の深さ 求め方まで、地震の計算の基本を解説してきました。この知識は、単にテストで高得点を取るためだけでなく、災害時に役立つ**防災の知識**でもあります。

地震発生時に緊急地震速報が鳴るメカニズムは、まさにP波とS波の速度差を利用したものです。P波を素早くキャッチし、そのデータから震源からの距離を計算し、その後に到達する破壊的なS波の到達時刻を予測しているのです。震源 距離 求め方の基本を理解していれば、速報の重要性や、速報が鳴ってから猶予時間が生まれる理由が明確にわかります。

知識と行動の結びつき

• 初期微動継続時間が長かった場合、遠方の地震であり、慌てずに落ち着いて行動できる。
• 初期微動継続時間が短かった場合、震源が近いことを瞬時に理解し、すぐに身を守る行動（シェイクアウト）に移れる。

このように、地震の計算をマスターすることは、自然災害に対する理解を深め、自分自身や大切な人を守るための確かな判断力を養うことにつながります。

震源 距離 求め方を学ぶことの総まとめ

これまでの解説を通して学んだ、地震の震源 距離 求め方に関する重要なポイントをリストでまとめます。

• 震源からの距離を求める基本はP波とS波の速度差を利用すること
• P波は縦揺れの初期微動、S波は横揺れの主要動を引き起こす
• 初期微動継続時間はP波とS波の到達時間の差であり震源距離に比例する
• 震源距離は初期微動継続時間に約8を掛ける簡易公式で推定可能である
• 正確な距離を求めるにはP波とS波の速度を2地点のデータから導出する必要がある
• P波の速度は観測点間の距離の差をP波到達時刻の差で割って計算する
• 震源からの距離 計算式は「速度 × 到達時間」の基本公式が適用される
• 地震発生時刻 求め方はP波到達時刻から到達時間を逆算して求める
• 震源の深さ 求め方には震源距離と震央距離を用いた三平方の定理が応用される
• 計算ミスを防ぐために時刻と時間、単位の変換に常に注意を払うことが重要である
• 比例式を利用した震源からの距離 求め方 公式はP波・S波の速度が不明な場合に有効である
• これらの計算の知識は緊急地震速報のメカニズムの理解に直結し防災意識を高める