P波とS波の速さの求め方を徹底解説！中学生にもわかる計算問題のコツとは
P波とS波の速さの求め方を徹底解説！中学生にもわかる計算問題のコツとは
地震の学習において、P波 S波 速さ 求め方は、多くの人が苦手意識を持つ計算分野の一つかもしれません。特に、異なる地点の観測データからP波 の求め方や、S波の速度求め方を導き出す問題は、複雑に感じられがちです。なぜなら、単に「地震 速さ 求め方」という公式を覚えるだけでなく、初期微動と主要動を引き起こすそれぞれの波の性質（速度 なぜ違うのか）を理解する必要があるからです。
この記事では、防災士の視点から、この難しい計算問題の克服をサポートします。まず、P波とS波の正式名称と違いを明確にし、P波とS波の覚え方は？といった基本的な用語解説から始めます。その上で、観測データが示すグラフの読み取り方、初期 微動 継続時間 求め方、そして震源からの距離や震源からの距離 求め方といった要素をどのように計算に活かすかを丁寧に解説します。
最終的には、P波 S波 速さ 問題を解くための実践的な手順とコツをマスターし、自信を持って地震の計算問題に取り組めるようになることを目指します。
この記事を読むことで以下のことがわかります
- P波とS波の基本的な違いと覚えるためのコツがわかる
- 異なる2地点のデータを使ったP波とS波の速さの計算方法がわかる
- 震源からの距離や地震発生時刻を求める応用問題の解き方がわかる
- 地震の速さに関する計算問題を解く上での注意点とコツが身につく
中学生でもわかるP波 S波 速さ 求め方の基本
- P波とS波の正式名称と性質を解説
- P波とS波の覚え方は？
- P波とS波で速度がなぜ違うのか
- 地震の速さの公式と計算の基本
- P波 の求め方：距離と時間の差を利用
- S波の速度求め方：P波と同じ手順で
P波とS波の正式名称と性質を解説
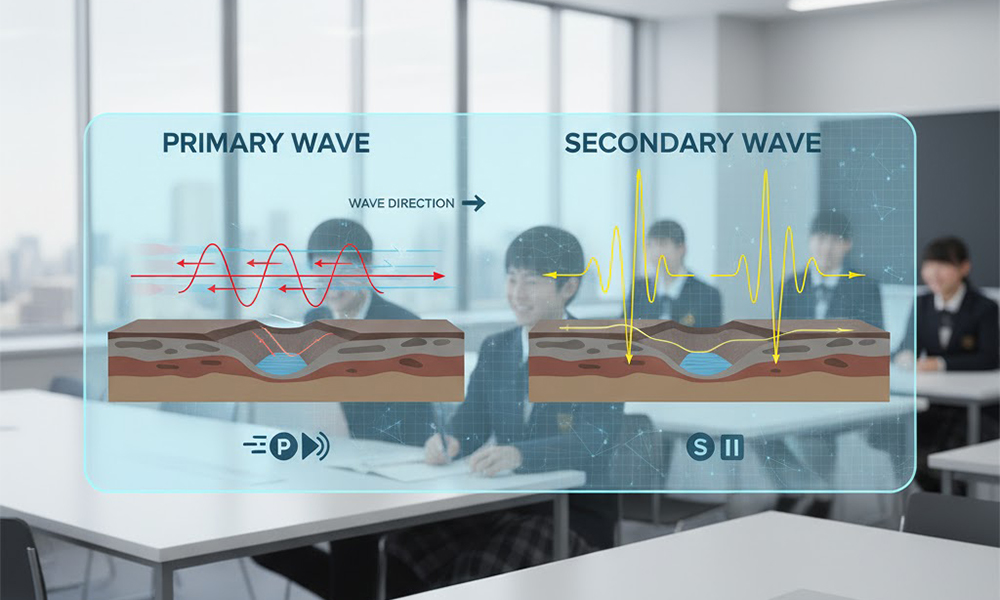
地震が発生した際に生じる揺れは、主に性質の異なる2つの波によって引き起こされます。これらがP波とS波です。P波は「Primary wave（プライマリー・ウェーブ）」の略で、日本語では「初期微動」と呼ばれる小さな揺れを引き起こします。
一方、S波は「Secondary wave（セカンダリー・ウェーブ）」の略で、P波の後に到達し、揺れ幅の大きい「主要動」を引き起こします。これらは地震計の記録から、到達時刻を正確に特定することが可能です。このように、P波が先に、S波が後に到達することが、両者の最も重要な違いです。
このP波とS波は、地震発生時に同時に震源から発生していますが、伝わる速さが異なるため、到達時刻に差が生じるのです。
| 波の名称 | 正式名称 | 引き起こす揺れ | 伝わる速さ（目安） |
|---|---|---|---|
| P波 | Primary wave（プライマリー・ウェーブ） | 初期微動（小さな揺れ） | 約6～8km/s |
| S波 | Secondary wave（セカンダリー・ウェーブ） | 主要動（大きな揺れ） | 約3～5km/s |
P波とS波の覚え方は？
P波とS波の違いや特徴は、いくつかの簡単なイメージで覚えることができます。一つはアルファベットの順番です。アルファベット順で「P」が「S」よりも先にくるため、P波が先に到着し、S波が後に到着すると覚える方法があります。実際、Pは「最初の」、Sは「2番目の」という意味を持つ正式名称の略です。
また、それぞれの特徴を人に見立てて覚える方法も非常に有効です。例えば、足が速く揺れが小さいP波を「痩せたP君：足が速いが、力は弱い」と覚え、足が遅く揺れが大きいS波を「太ったS君：足は遅いが、力は強い」と覚える方法があります。これにより、P波が速い（速さ：6～8km/s）が揺れが小さいこと、S波が遅い（速さ：3～5km/s）が揺れが大きい（主要動）ことが視覚的にイメージしやすくなります。
P波とS波で速度がなぜ違うのか
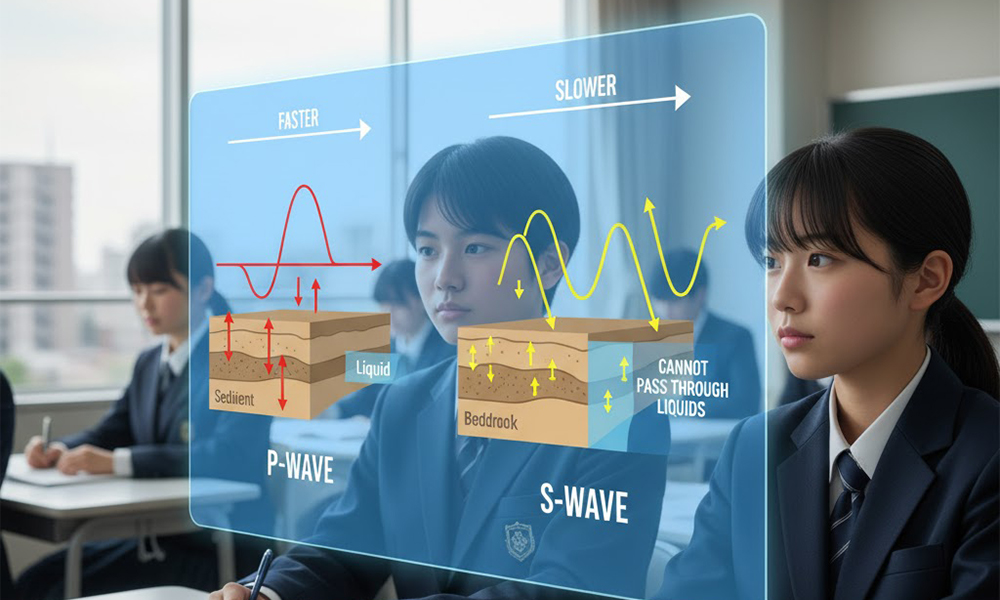
P波とS波の速度が異なる理由は、それぞれの波が地面を伝わる仕組み（波の性質）が違うからです。P波は、波が伝わる方向と同じ方向に地面を振動させる「縦波」です。音波と同じような伝わり方をするため、固体・液体・気体のあらゆる物質の中を伝わることができます。
一方、S波は、波が伝わる方向に対して垂直に地面を振動させる「横波」です。この横波は、液体や気体の中では伝わることができず、主に固体の中を伝わります。縦波であるP波の方が、固体（岩盤）を効率よく伝えることができるため、S波よりも速く伝わるという性質を持っています。これが、P波が速く、S波が遅い主な理由です。
地震の速さの公式と計算の基本
地震の波の速さを求める計算は、小学校の算数で習う「速さの公式」と同じものを使います。つまり、速さ＝距離÷時間の公式に当てはめて計算を進めます。
地震 速さ 求め方 公式
$$地震の速さ (\text{km/s}) = \frac{\text{震源距離} (\text{km})}{\text{伝わるのにかかった時間} (\text{秒})}$$
ここで最も重要な注意点は、問題文に記載されている時刻をそのまま時間として使ってはいけないことです。多くのP波 S波 速さ 問題では、観測時刻が与えられます。しかし、計算で必要なのは「波が震源から観測点まで伝わるのにかかった時間」です。
したがって、観測時刻から地震発生時刻を引くことで、この「伝達時間」を正確に求めなければなりません。もし、地震発生時刻が不明な場合は、異なる2地点の観測データを利用して「距離の差 ÷ 時刻の差」で速さを求めることになります。
P波 の求め方：距離と時間の差を利用
P波の速さは、基本的にP波が到達した時刻のデータを使って計算します。もし地震発生時刻が不明な場合は、異なる2地点の観測データを使ってP波の速さを求めるのが一般的です。この方法は、「距離の差 ÷ 時刻の差」を用いることで、発生時刻の影響を打ち消して速さだけを正確に算出できます。
P波 の求め方の計算手順
- 異なる2地点（例：A地点とB地点）の震源からの距離の差を求める。
- A地点とB地点のP波（初期微動）到着時刻の差を求める。
- P波の速さ ＝ （距離の差）÷（P波到着時刻の差）を計算する。
例えば、A地点（距離$84$km、P波時刻$2$分$00$秒）とB地点（距離$168$km、P波時刻$2$分$14$秒）のデータを用いる場合を考えてみましょう。距離の差は$168 \text{km} – 84 \text{km} = 84 \text{km}$です。時間の差は$2$分$14$秒 $- 2$分$00$秒 $= 14$秒です。したがって、P波の速さは$84 \text{km} \div 14 \text{秒} = 6 \text{km/秒}$と求められます。
S波の速度求め方：P波と同じ手順で
S波の速度求め方も、P波の求め方と全く同じ手順で行います。ただし、計算に用いるのはS波の到達時刻のデータです。
S波の速度求め方の計算手順
- 異なる2地点（例：A地点とB地点）の震源からの距離の差を求める（P波と共通）。
- A地点とB地点のS波（主要動）到着時刻の差を求める。
- S波の速さ ＝ （距離の差）÷（S波到着時刻の差）を計算する。
前述の通り、S波はP波よりも遅く伝わるため、計算結果として得られるS波の速さの値は、P波の速さよりも小さくなるはずです。例えば、S波がA地点に$2$分$08$秒、B地点に$2$分$28$秒に到達したと仮定すると、時間の差は$20$秒です。距離の差の$84 \text{km}$を用いて計算すると、S波の速さは$84 \text{km} \div 20 \text{秒} = 4.2 \text{km/秒}$となります。このように、P波よりも遅い値になることを確認することも、計算ミスを防ぐ上での重要なチェックポイントです。
観測データを使ったP波 S波 速さ 求め方の応用
- 地震の観測データとグラフの見方
- 初期 微動 継続時間の求め方とは
- 震源からの距離の求め方と速さの関係
- 地震発生時刻の計算方法
- 応用：P波 S波 速さ 問題に挑戦
- P波 S波 速さ 求め方：計算のコツとまとめ
地震の観測データとグラフの見方
地震の計算問題では、地震の観測データとグラフが重要な情報源となります。観測データは、表形式で「観測点、震源からの距離、初期微動が始まった時刻、主要動が始まった時刻」などが示されることが多くあります。これらの数値は、P波とS波の速さ、地震発生時刻などを求めるための具体的な材料となります。
また、縦軸に「震源からの距離」、横軸に「地震発生からの時間」をとったグラフが用いられることもあります。このグラフには、P波の到達を示す線（傾きが急）と、S波の到達を示す線（傾きが緩やか）の二本が描かれています。P波とS波それぞれの線上で、任意の距離に対応する時間を読み取ることで、速さ＝距離÷時間の計算に利用できるのです。特に、2本の線の間の縦軸上での距離が一定の時間差（初期微動継続時間）となるため、このグラフから多くの情報が得られます。
初期 微動 継続時間の求め方とは
初期 微動 継続時間 求め方は、非常にシンプルです。これは「初期微動が続く時間」を指しており、言い換えれば「P波が到着してからS波が到着するまでの時間」のことです。
したがって、観測地点におけるS波（主要動）の開始時刻からP波（初期微動）の開始時刻を引けば求めることができます。例えば、P波が$10$時$15$分$18$秒に到達し、S波が$10$時$15$分$33$秒に到達した場合、初期微動継続時間は$33$秒 $- 18$秒 $= 15$秒となります。
初期微動継続時間の求め方
初期微動継続時間$=$主要動開始時刻$ – $初期微動開始時刻
この時間は、震源からの距離に比例するという重要な性質を持っています。なぜなら、P波とS波の速度差（P波の方がS波より速い）は一定であるため、伝わる距離が長くなるほど、両者が到着する時間の差（初期微動継続時間）も大きくなるからです。
震源からの距離の求め方と速さの関係
震源からの距離 求め方は、速さ＝距離÷時間の公式を変形して、距離＝速さ × 時間を使うことで求められます。ただし、ここで使用する「時間」は、その波が震源から観測点まで伝わるのにかかった時間、つまり「伝達時間」でなければなりません。
震源からの距離の求め方
震源からの距離$=$P波（またはS波）の速さ$ \times $P波（またはS波）が伝わるのにかかった時間
前述の通り、P波が伝わるのにかかった時間は「P波到着時刻 $-$ 地震発生時刻」で計算します。もし、地震発生時刻が不明な場合は、P波とS波の速度差と初期微動継続時間から距離を求める複雑な計算（比例式など）が必要になります。
地震発生時刻の計算方法
地震発生時刻は、P波の速さと震源からの距離がわかっている場合に、P波の到着時刻から伝達時間を引くことで求められます。これは、P波が観測点に到達した時刻よりも、P波が伝達にかかった時間分だけ前に地震が発生しているからです。
地震発生時刻の求め方
- P波の伝達時間$=$震源からの距離 $\div $ P波の速さを計算する。
- 地震発生時刻$=$P波到着時刻$ – $P波の伝達時間を計算する。
例えば、震源からの距離$80 \text{km}$の地点でP波が$12$時$24$分$53$秒に到達し、P波の速さが$5.7 \text{km/秒}$とわかっている場合を考えてみましょう。まず、伝達時間を$80 \text{km} \div 5.7 \text{km/秒} \approx 14 \text{秒}$と算出します。そして、到着時刻からこの$14$秒を引けば、$12$時$24$分$53$秒 $- 14$秒 $= 12$時$24$分$39$秒が地震発生時刻となります。
注意点
S波のデータからも地震発生時刻を求めることは可能ですが、S波の速度はP波の速度よりも正確に求めにくい場合もあるため、P波のデータを使って計算する方がより確実とされています。
応用：P波 S波 速さ 問題に挑戦
P波 S波 速さ 問題では、通常、速さの計算だけでなく、震源からの距離、地震発生時刻、初期微動継続時間といった様々な要素を複合的に求めることが要求されます。これらの応用問題を解くには、まずP波とS波の速さを正確に求め、それを基に逆算していくのがコツです。
具体的な問題として、観測点Cの主要動開始時刻や、観測点Dの震源からの距離が不明な場合を考えてみましょう。このような応用問題では、まず既知の2地点（AとBなど）のデータからP波とS波の速さを求め、次に地震発生時刻を算出するという手順を踏むのが鉄則です。
速さと発生時刻がわかれば、他の地点の不明なデータ（主要動開始時刻や震源からの距離）は、距離＝速さ × 時間、または時間＝距離 ÷ 速さといった基本的な公式で全て算出できます。この段階的なアプローチを習得することが、応用問題を解く鍵となります。
P波 S波 速さ 求め方：計算のコツとまとめ
地震のP波 S波 速さ 求め方に関する計算問題は、焦らずに手順を追って進めることで、必ず解くことができます。最も重要なのは、「時刻」と「時間」の違いを理解し、距離の差と時間の差を使うことで、正確な速さを導き出すことです。
これらの理由から、複雑な問題も分解して考えることが大切です。ここで、記事全体の内容と計算のコツをリスト形式で整理し、確認しましょう。
- P波とS波は同時に発生するが、P波の方が速い
- P波は初期微動、S波は主要動を引き起こす
- 速さの公式は「速さ＝距離÷時間」であり、算数と同じ考え方で計算できる
- P波とS波の速さを求めるには「距離の差 ÷ 到着時刻の差」を用いる
- P波の速さはS波の速さより必ず大きくなることを確認する
- 初期微動継続時間は「主要動開始時刻 $-$ 初期微動開始時刻」で求められる
- 震源から遠くなるほど初期微動継続時間は長くなる
- 地震発生時刻は「P波到着時刻 $-$ P波の伝達時間」で逆算する
- 伝達時間は「震源からの距離 $\div $ P波の速さ」で計算する
- 震源からの距離は「速さ $\times $ 伝達時間」で計算する
- 応用問題は「速さ $\rightarrow$ 発生時刻 $\rightarrow$ その他」の順で解くのが基本
- 計算には「時刻」ではなく「伝わるのにかかった時間」を使うことが重要
コメント