小学生向け！てこの原理をわかりやすく防災視点で解説

「てこの原理ってなに？」と疑問に思っている小学生のみなさん、こんにちは。理科の授業で「てこの原理」という言葉を聞いたけれど、計算が出てきそうで難しそう、種類が多くて混乱する、と感じているかもしれません。てこの原理は、支点・力点・作用点という3つの基本的なポイントを理解することがスタートです。この記事では、てこの原理を小学生にもわかりやすい言葉で、図や具体例を交えながら解説します。

シーソーのような簡単な例から、てこの長さと力の関係を知ろうとすると、力のつり合いに関する計算が必要になることもあります。しかし、基本のルールさえ押さえれば決して難しくありません。実は、てこの原理を使った道具は私たちの身近な生活にあふれています。ぜひ、この記事を読みながら、身近にあるてこの道具を探そうとしてみてください。この記事を読めば、実験でわかる、力が小さくても動く秘密がきっと理解できるはずです。

そして、てこの3つの大事なポイントを学んだ最後には、防災で活躍！てこの原理でできることについても詳しく触れていきます。てこの原理は、理科のテストのためだけでなく、いざという時に自分や周りの人を助ける「生きる力」にもなる大切な知識なのです。

• てこの原理の基本的な3つの要素（支点・力点・作用点）がわかる
• 「力のモーメント」を使った簡単な計算方法が身につく
• 身近な道具がどの種類のてこに当てはまるか理解できる
• 防災現場で「てこ」がどのように役立つかを知ることができる

小学生向け！てこの原理がわかるやすい解説

• そもそも、てこの原理ってなに？
• てこの原理の支点・力点・作用点
• 覚えるのは３つ！てこの3つの大事なポイント
• 実験でわかる！力が小さくても動く秘密
• てこの長さと力の関係を知ろう
• 簡単！てこのつり合いの計算

そもそも、てこの原理ってなに？

てこの原理とは、ひとことで言えば「小さな力で大きな力を生み出すためのしくみ」のことです。物理の基本的な原理のひとつで、これがあるおかげで、私たちは自分一人の力ではとても動かせないような重い物を動かすことができます。

一番イメージしやすいのは、公園にあるシーソーです。例えば、自分よりもずっと体重が重いお父さんやお母さんとシーソーに乗る時を想像してください。もし二人が支点（真ん中の軸）から同じ距離の場所に座ったら、体重が重い方が下に下がってしまい、つり合いませんよね。

でも、お父さんやお母さんに中心（支点）のなるべく近くに座ってもらい、自分が端っこの方（支点から遠い場所）に座れば、体重が軽くてもつり合わせることができ、シーソーで遊ぶことができます。

このように、重い人（大きな力）でも、支点からの「距離」を短くすれば、軽い人（小さな力）が支点から「距離」を長くすることで、つり合わせることが可能になります。この「力と距離の関係」こそが、てこの原理の基本的な考え方です。

豆知識：アルキメデスの言葉

古代ギリシャの科学者アルキメデスは、「私に支点を与えてくれ。そうすれば地球すら動かしてみせよう」という言葉を残したと伝えられています。（※伝説という説もあります）

これは、「どれだけ重いものでも、支点からの距離をものすごく長くした『てこ』を使えば、小さな力で動かせる」という、てこの原理の可能性を示した言葉です。それほど、てこの原理は強力なしくみなのです。

てこの原理の支点・力点・作用点

てこの原理をマスターするためには、絶対に欠かせない3つの基本的なポイントがあります。それが「支点（してん）」「力点（りきてん）」「作用点（さようてん）」です。この3つの言葉は必ず覚えてください。

• 支点（してん）：
  てこを支える点のこと。棒や板が回転するときの「中心軸」になります。シーソーの真ん中の軸、ハサミの真ん中の留め具がこれにあたります。
• 力点（りきてん）：
  人が力を加える点のこと。「力を入れる場所」です。シーソーで人が座る場所、ハサミの持ち手の部分（指を入れる輪）です。
• 作用点（さようてん）：
  てこの力が実際に「はたらく」点のこと。「力が伝わる場所」です。シーソーの反対側で持ち上げられる相手が座る場所、ハサミで紙を切る刃の部分を指します。

この3つの点の「位置関係」（どこに支点があり、どこに力点と作用点があるか）によって、てこは大きく3種類に分類されます。身の回りの道具がどの種類にあたるのかを考えることは、てこをマスターする上でとても大切になります。

覚えるのは３つ！てこの3つの大事なポイント

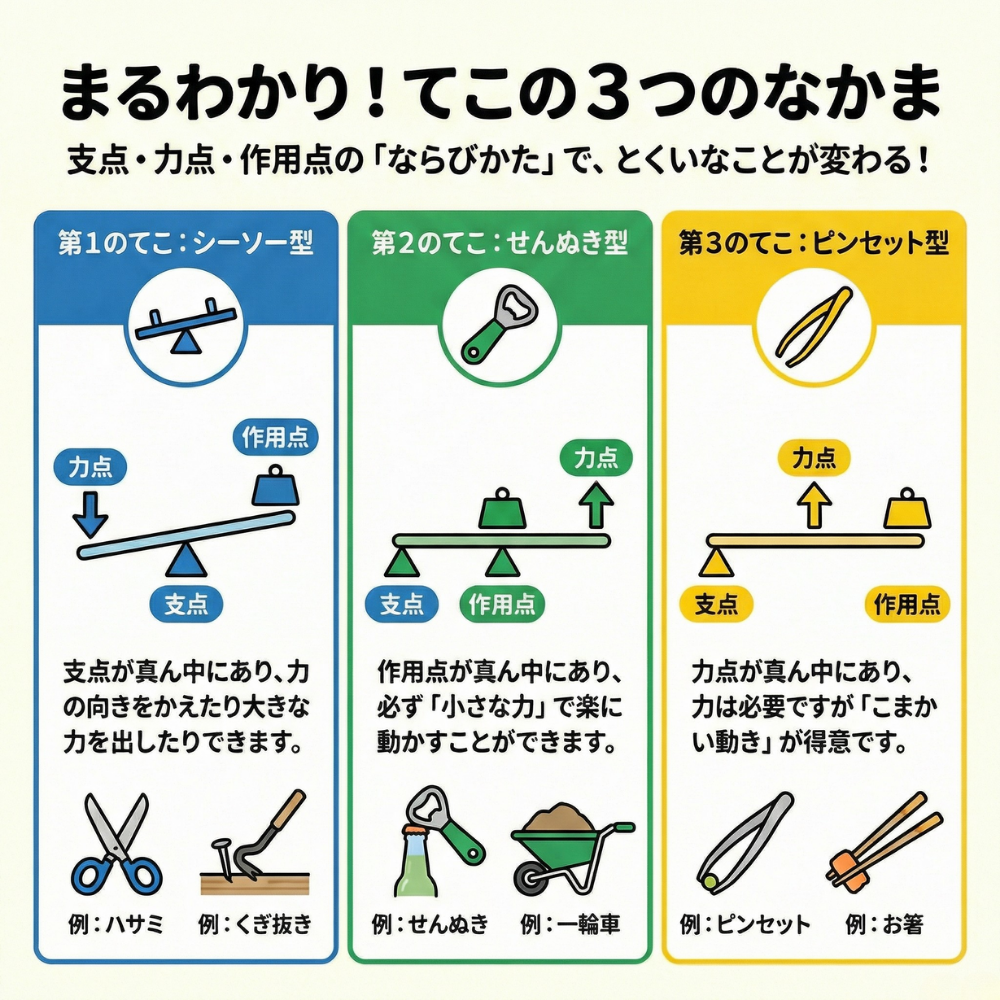
てこは、前述の通り、支点・力点・作用点の3つの点の位置関係によって、大きく3種類に分類されます。それぞれの特徴を、具体的な道具と一緒に見ていきましょう。

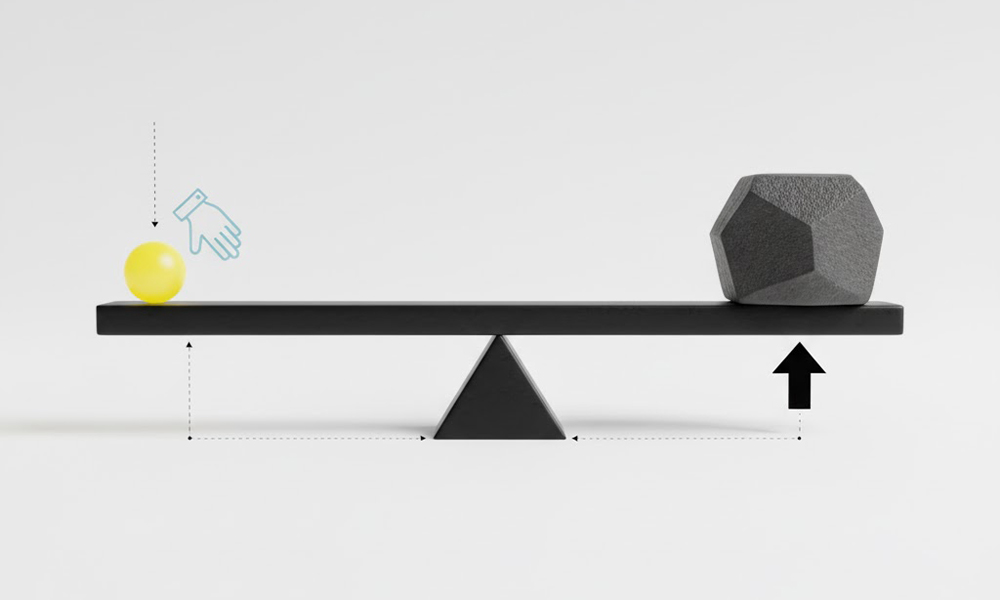
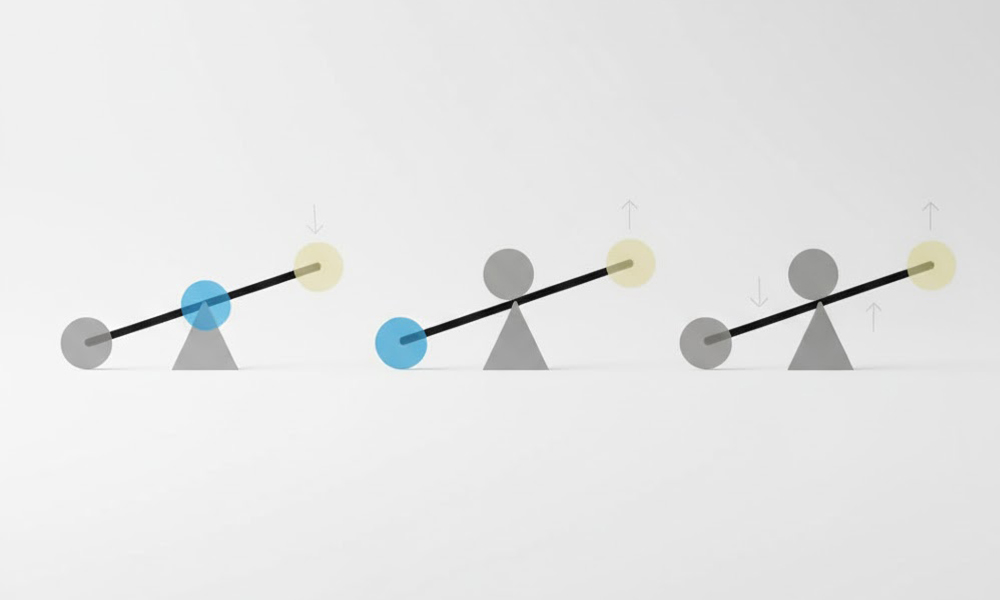
第1のてこ（シーソー型）

特徴：支点が、力点と作用点の間にある。（力点 ― 支点 ― 作用点）

最も基本的でイメージしやすいタイプが「第1のてこ」です。シーソーや、くぎ抜き、ペンチ、洋ばさみ（一般的なハサミ）などがこれにあたります。

このタイプは、支点を中心にして、力点と作用点が反対側にあります。大きな特徴は、「力点を支点から遠くするほど、作用点で大きな力を出せる」ことです。くぎ抜きは、手で持つ部分（力点）が、くぎを抜く部分（作用点）よりも支点からずっと遠くにあるため、硬い釘でも小さな力で引き抜けます。

逆に、力点を支点に近づけると、作用点で出せる力は小さくなります。

第2のてこ（せんぬき型）

特徴：作用点が、支点と力点の間にある。（支点 ― 作用点 ― 力点）

「第2のてこ」の代表例は、瓶のフタを開ける「せんぬき」です。他にも、荷物を運ぶ一輪車や、紙に穴を開ける穴あけパンチもこのタイプに含まれます。

このタイプは、図を見てもわかる通り、常に力点（力を加える点）の方が、作用点（力がはたらく点）よりも支点から遠くなります。支点からの距離が「力点 ＞ 作用点」となるため、必ず小さな力で大きな力を生み出すことができるのが最大のメリットです。必ず「力」の面で得をする、便利なタイプと言えます。

第3のてこ（ホッチキス型・ピンセット型）

特徴：力点が、支点と作用点の間にある。（支点 ― 力点 ― 作用点）

「第3のてこ」は、ピンセットやトング、ホッチキス、和ばさみ（糸切りばさみ）、そして人間の腕（肘を支点とした場合）などが当てはまります。

このタイプは、他の2つとは全く逆の性質を持っています。力点（力を加える点）が作用点（力がはたらく点）よりも支点に近いため、作用点ではたらく力は、力点で加えた力よりも小さくなってしまいます。「小さな力で大きな力を出す」という目的には合わず、力の面では「損」をしてしまいます。

第3のてこは力が小さくなる（損する）のに、なぜ使うの？

それは、「動きを大きくできる」という大きなメリットがあるからです。例えばピンセットで、手元の力点をほんの少し動かすだけで、先端の作用点はそれよりも大きく動きます。これにより、小さな物をつかんだり、細かい作業をしたりすることが可能になるのです。

力を犠牲にする代わりに、「動きの幅（可動域）やスピード」を得ているのが第3のてこです。お箸や釣竿もこの仲間です。

これら3種類のてこをまとめた表が以下になります。道具と3点の位置関係をセットで覚えると効果的です。

種類	3点の位置関係	特徴	主な道具
第1のてこ	力点 ― 支点 ― 作用点	・力を大きくも小さくもできる ・力の向きが変わる	シーソー、くぎ抜き、ハサミ、ペンチ、ラジオペンチ
第2のてこ	支点 ― 作用点 ― 力点	・必ず力は大きくなる（得） ・力の向きは変わらない	せんぬき、一輪車、穴あけパンチ、缶切り
第3のてこ	支点 ― 力点 ― 作用点	・必ず力は小さくなる（損） ・動きは大きくなる（得）	ピンセット、トング、ホッチキス、和ばさみ、釣竿、お箸、腕

実験でわかる！力が小さくても動く秘密

てこの原理で「小さな力で大きな力を生み出す」秘密は、支点からの「距離」にあると説明しました。これは簡単な実験ですぐに体感できます。

一番わかりやすいのは、ドアを開ける時です。ドアノブは、ドアの開け閉めの軸である「ちょうつがい（これが支点）」から一番遠い場所についていますよね。ドアノブ（力点）を押せば、軽い力でドア（作用点はドア全体）を開け閉めできます。

では、ちょうつがいのすぐ近く（支点の近く）を押してみてください。ドアはとても重く感じ、開けるのにかなりの力が必要になるはずです。

このように、支点から力を加える場所（力点）までの距離が長ければ長いほど、作用点で発揮できる力は大きくなります。逆に、距離が短いと大きな力が必要になるのです。

（家でできる簡単実験）

30cmくらいの定規と、消しゴム（支点用）、そしてコイン（おもり用）を用意してみましょう。

1. まず、定規の15cmの目盛りの下に消しゴム（支点）を置きます。
2. 定規の端（例：30cmの場所）にコインを1枚（作用点）置きます。
3. 反対側の端（例：0cmの場所）を指（力点）で押して、コインを持ち上げてみてください。

次に、消しゴム（支点）をコインのすぐ近く（例：25cmの場所）に動かしてみましょう。 同じように反対側の端（0cmの場所）を指で押すと…どうでしょうか？
さっきよりも圧倒的に軽い力でコインが持ち上がるはずです。これが「支点から力点までの距離を長くした」効果です！

てこの長さと力の関係を知ろう

では、「距離」と「力」には、具体的にどのような計算上の関係があるのでしょうか。この関係を表すために登場するのが「力のモーメント」という、とても大事な考え方です。

力のモーメントとは、物体を「回転させようとする力のはたらき（能力）」の大きさを表す数値です。言葉は少し難しいですが、計算はとても簡単な「かけ算」です。

力のモーメント ＝ 支点からの距離 × 力（おもりの重さなど）

例えば、支点から50cmの場所につるした100gのおもりがあるとします。 このおもりが生み出す力のモーメントは、

50cm × 100g = 5000

となります。

この「5000」という数値が、てこを回転させようとする力の強さを示しています。単位は中学受験などでは難しく考えず、「g・cm（グラムセンチメートル）」のように、かけた単位をそのまま付けておけば大丈夫です。

この数値が大きければ大きいほど、「回転させる力が強い」ということになります。

簡単！てこのつり合いの計算

てこが「つり合う」とは、どういう状態でしょうか。 それは、支点を中心にして「時計回りに回そうとする力」と「反時計回りに回そうとする力」がぴったり等しくなった状態です。

力のモーメントを使って表すと、以下の「つり合いの式」が成り立ちます。てこの計算は、すべてこの式で解くことができます。

つり合いの式：
時計回りのモーメントの合計 ＝ 反時計回りのモーメントの合計

例えば、下の図のように、支点の左側（反時計回り）40cmの場所に？gのおもりがあり、右側（時計回り）30cmの場所に200gのおもりがあってつり合っているとします。

この場合、それぞれのモーメントを計算すると、

・時計回りのモーメント： 30cm × 200g ＝ 6000
・反時計回りのモーメント： 40cm × ？g

この２つが「＝（イコール）」になるはずなので、「40 × ？ ＝ 6000」という式が作れます。 ここから、？（おもりの重さ）を求めることができます。

？ ＝ 6000 ÷ 40 ＝ 150g

このように、てこがつり合う計算は、モーメントのかけ算と割り算だけで解くことができます。

おもりが複数ある場合は？

おもりが複数あっても考え方は同じです。「合計」で比べればOKです。

（例）支点の左 20cmに50g、左 40cmに30gのおもりがあり、右 50cmに？gのおもりがあってつり合う場合。

・反時計回り（左側）のモーメント合計：
(20cm × 50g) ＋ (40cm × 30g) = 1000 + 1200 = 2200

・時計回り（右側）のモーメント合計：
50cm × ？g

つり合うので、「50 × ？ = 2200」
？ = 2200 ÷ 50 = 44g となります。

てこの原理が小学生にもわかりやすい応用編

• これも！てこの原理を使った道具たち
• 身近にあるてこの道具を探そう！
• 防災で活躍！てこの原理でできること
• てこの原理を小学生にわかりやすく解説

これも！てこの原理を使った道具たち

私たちの身の回りには、本当にたくさんの道具にてこの原理が使われています。先ほど紹介した3種類のてこが、他にどのような道具で使われているか、さらに詳しく見てみましょう。

第1のてこ（支点が真ん中：力点 ― 支点 ― 作用点）
・くぎ抜き：支点はヘッド（頭）の部分、力点は持つ場所、作用点はくぎが刺さっている場所です。
・ペンチ／ラジオペンチ：支点は真ん中の留め具、力点は握る場所、作用点は物をつかむ先端です。
・上皿てんびん：支点は真ん中の軸、力点と作用点は左右の皿です。これはモーメントをつり合わせる道具そのものです。

第2のてこ（作用点が真ん中：支点 ― 作用点 ― 力点）
・せんぬき：支点はフタの端、力点は手で持つ場所、作用点はフタの真ん中です。
・穴あけパンチ：支点は端の軸、力点は手で押す場所、作用点は紙に穴を開ける刃の部分です。
・自転車のブレーキ（ハンドル側）：支点はハンドルの付け根、力点は指で握るレバーの先端、作用点はワイヤーを引く部分です。（※ブレーキ本体も別種のてこです）

第3のてこ（力点が真ん中：支点 ― 力点 ― 作用点）
・ピンセット／トング：支点はお尻のつながった部分、力点は指で持つ真ん中あたり、作用点は物をつかむ先端です。
・ホッチキス：支点は後ろの軸、力点は手で押す場所、作用点は針が出る先端です。
・人間の腕：肘を支点、力こぶ（筋肉）が力を出す場所を力点、手のひらに物を持った場所を作用点と考えることができます。

このように、道具がどのタイプのてこを使っているかを知ることで、その道具が「力を大きくすること」を目的にしているのか、「動きを大きくすること」を目的にしているのかがはっきりと分かります。

身近にあるてこの道具を探そう！

てこを使った道具は、学校の教室や家の中、公園など、探せばもっとたくさん隠れています。ぜひ、自分で「これはてこだ！」というものを探し、さらに「第何てこか？」を分類してみてください。

（先生より）
例えば、みんなが毎日使っている「爪切り」はどうでしょうか？
爪切りは、実は「第1のてこ（持ち手部分）」と「第2のてこ（刃の部分）」が組み合わさってできています。複数のてこを組み合わせることで、あんなに硬い爪でも軽い力でパチンと切ることができる、非常に優れた道具なのです。

他にも、窓の鍵（クレセント錠）や、蛇口のハンドル、自転車のブレーキレバー、体育館のバスケットゴールを（壁から）出す時のハンドルなども、てこの原理を応用したものです。
身の回りの道具を「支点・力点・作用点」の3つの目で見てみると、たくさんの発見があるはずですよ。

防災で活躍！てこの原理でできること

てこの原理は、日常生活を便利にするだけでなく、いざという時に人の命を助けるためにも使われます。これが、防災士の視点から最も伝えたい「てこの原理」の重要な役割です。

例えば、大きな地震が起きて、タンスや本棚が倒れたり、ブロック塀が崩れたりして、もし誰かがその下敷きになってしまったら…大人の力でも、数百kgにもなる重い家具やコンクリートのブロック塀をそのまま持ち上げるのは非常に困難です。

救助の現場で「てこ」が大活躍！

このような緊急事態では、消防や救助隊が到着するまでの間、周りにいる人たちで助け出さなければなりません（これを「共助」といいます）。その時、てこの原理が大きな力を発揮します。

バール（かなてこ）や丈夫な角材、鉄パイプなどを「てこ」として使います。 倒れた家具やブロック塀のすき間に角材を差し込み（作用点）、支点となる丈夫な石や別の角材を近くに置きます（支点）。そして、角材のできるだけ端（力点）に体重をかけることで、作用点であるブロック塀の端を少しだけ持ち上げることができるのです。

（参考：東京消防庁「救出・救護」）

たった数センチのすき間を作るだけでも、下敷きになった人の痛みを和らげたり、体を引き出すスペースを作ったりすることができます。これはまさに「第1のてこ」の応用です。

また、車のタイヤ交換に使う「ジャッキ」も、てこやネジの原理を応用して、1トン以上ある重い車体を持ち上げる道具です。防災現場では、このような専用の救助器具が使われることもあります。

もちろん、最も大切なのは、地震が起きても家具が倒れないように固定しておくことです（予防）。東京消防庁のサイトなどでは、家具の転倒防止対策を紹介していますので、ぜひお家の人と確認してみてください。

てこの原理は、理科の勉強であると同時に、自分や大切な人を守るための「生きる力」そのものなのです。

てこの原理を小学生にわかりやすく解説

この記事では、てこの原理の基本から防災での応用までを、小学生にもわかりやすい視点で解説しました。最後に、大切なポイントをまとめます。

• てこの原理は小さな力で大きな力を生み出すしくみ
• てこには「支点」「力点」「作用点」の3つの点がある
• 支点はてこを支える中心の点
• 力点は人が力を加える点
• 作用点はてこの力がはたらく点
• 3点の位置関係で「第1のてこ」「第2のてこ」「第3のてこ」に分かれる
• 第1のてこは支点が真ん中（例：シーソー、ハサミ、くぎ抜き）
• 第2のてこは作用点が真ん中（例：せんぬき、一輪車）
• 第2のてこは必ず力が大きくなる（力で得をする）
• 第3のてこは力点が真ん中（例：ピンセット、ホッチキス、お箸）
• 第3のてこは力が小さくなるが、動きが大きくなる（動きで得をする）
• 支点から力点までの距離が遠いほど、発揮できる力は大きくなる
• 回転させようとする力の能力を「力のモーメント」という
• 力のモーメントは「支点からの距離 × 力」で計算できる
• てこがつり合うのは「時計回りのモーメントの合計＝反時計回りのモーメントの合計」の時
• おもりが複数あっても「合計」で考えれば計算できる
• 爪切りや穴あけパンチなど、身近な道具に多く使われている
• 地震などで重いものの下敷きになった人を救助する際にもてこは活躍する
• バールや角材を「第1のてこ」として使い、すき間を作ることができる
• てこの原理は、理科の勉強であり、命を助ける「防災の知恵」でもある