ドップラー効果をわかりやすく!救急車から防災まで仕組みを解説

ドップラー効果をわかりやすく!救急車から防災まで仕組みを解説
こんにちは。「ふくしまの防災 HIH ヒカリネット」防災士の後藤です。
皆さんは、街中で救急車のサイレンを聞いたとき、音が劇的に変わる瞬間に立ち会ったことはありませんか?遠くから近づいてくるときは「ピーポーピーポー」と高く緊迫した音だったのに、自分の目の前を通り過ぎて遠ざかっていく瞬間に、急に「ヒューン」と力が抜けたような低い音に変わる、あの不思議な現象です。
実はこれ、物理の授業で必ず登場する「ドップラー効果」という現象なのですが、名前だけ聞いて「計算が難しそう」「物理は苦手」と身構えてしまう方も多いかもしれません。でも、安心してください。この原理は、単なるテスト勉強のための知識ではありません。実は、私たちの命を守る気象レーダーによる豪雨予測や、病院での精密検査など、意外と身近な場所で活躍している、とても頼もしい技術でもあるのです。
今回は、この少し不思議な音の仕組みや、テストで使える公式の考え方、そして光や最新の防災技術への応用について、専門用語をできるだけ使わずに、防災士の視点も交えながら噛み砕いてお話しします。
この記事でわかること
- 救急車のサイレン音が変化して聞こえる物理的な理由
- 音の高さが変わる仕組みと間違えやすいポイント
- テストや試験で役立つ公式の覚え方と計算のコツ
- 気象レーダーや医療など身近な技術への意外な活用法
ドップラー効果をわかりやすく基礎から解説

まずは、ドップラー効果がなぜ起こるのか、その根本的な仕組みから一緒に見ていきましょう。物理と聞くと難しく感じるかもしれませんが、要するに「音の波がどう伝わるか」という、とてもシンプルな話なんです。ここでは、よくある誤解を解きながら、直感的にイメージできるように解説します。
音の高さが変わる仕組みと原理

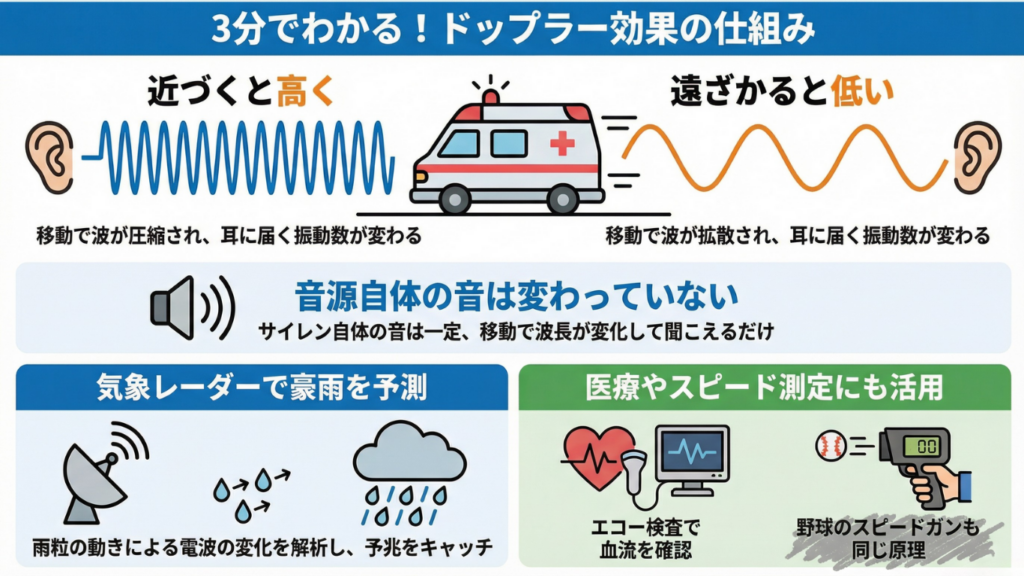
ドップラー効果を一言で説明すると、「音を出すモノ(音源)や聞く人(観測者)が動くことによって、音の波が伸び縮みして聞こえる現象」のことです。
そもそも「音」とは何でしょうか?音は、空気の振動が波となって伝わる現象です。この波の性質には、以下の2つの重要なルールがあります。
- 波がギュッと詰まる(波長が短い):高い音として聞こえる
- 波の間隔が広がる(波長が長い):低い音として聞こえる
ここで非常に大切なポイントがあります。それは、音源そのものが出している音の高さ(振動数)は、実は全く変わっていないという点です。救急車に乗っている隊員さんには、サイレンの音はずっと同じ高さで聞こえています。動いているのはあくまで物体であって、音そのものが変化しているわけではありません。
つまり、音源が動くことによって、私たちに届くまでの「波の形」が見かけ上、圧縮されたり引き伸ばされたりしてしまう。これがドップラー効果の正体なのです。
ここがポイント!
音源が進行方向に動くと、前方の波は「圧縮」されて波長が短くなり(=高音)、逆に後ろ側の波は「引き伸ばされて」波長が長く(=低音)なります。
救急車のサイレンで理解する例

最も有名な例といえば、やはり救急車のサイレンですね。サイレンを鳴らしながら自分に猛スピードで近づいてくる救急車を想像してみてください。
近づいてくるとき:音の波を追いかける
救急車が音を出しながら進むとき、自分が出した音の波を、自分自身で追いかけるような形になります。すると、進行方向にある空気の波は、救急車に後ろから押されるようにして、波と波の間隔が狭くなります。
波の間隔が狭いということは、私たちの耳(鼓膜)に到達する波の数が増えるということです。鼓膜を振動させる回数が多いほど、脳はそれを「高い音」として認識します。
遠ざかっていくとき:音の波を置き去りにする
逆に、救急車が通り過ぎて遠ざかっていくときはどうでしょうか。今度は音源が私たちから逃げていく形になります。救急車は音を出したそばから遠くへ行ってしまうため、後ろに残された音の波は、間隔が間延びして広くなってしまいます。
波の間隔が広いと、単位時間あたりに鼓膜に届く振動の回数が減り、結果として「低い音」に聞こえるのです。「ピーポーピーポー」という音が、目の前を通過した瞬間に「ヒューン」と情けない音に下がるのは、まさに波の密度がギュッと詰まった状態からスカスカの状態へ変わった瞬間を、耳で捉えているからなんですね。
ボール投げの例え話でイメージ

ドップラー効果を理解する上で、多くの人がつまづきやすい「誤解」があります。それは、「速く動いているものから出た音は、速く飛んでくる」と思ってしまうことです。これを正すために、キャッチボールで例えてみましょう。
ボールと音の決定的な違い
もし、時速100kmで走っているトラックの荷台から、投手が時速100kmでボールを前方に投げたとします。この場合、地面にいる人から見ると、ボールの速度は足し算されて時速200kmになります。これは直感的にわかりますよね。
しかし、音(波)の場合はこれが当てはまりません。
よくある間違いに注意!
ボールの場合は「投げる人の速度 + ボールの初速」になりますが、音の場合は音源がどれだけ速く動いても、音速は足し算されません。
音の速さ(約340m/s)は、空気という「媒質(ばいしつ)」の状態だけで決まります。空気が「音の運び屋さん」だと想像してください。運び屋さんの歩くペース(音速)は決まっていて、誰から荷物(音)を受け取っても、その歩くペース自体は変わらないのです。
ベルトコンベアのイメージ
これを正しく例えるなら、「一定の速度で動くベルトコンベアに、走りながら荷物を置いていく作業」が近いです。
- ベルトコンベアの速さ:音速(常に一定)
- 荷物を置く人:音源
- 荷物の間隔:波長
荷物を置く人が前方に走りながら荷物を置けば、ベルトコンベア上の荷物の間隔は狭くなります(波長が短くなる)。でも、ベルトコンベアが動く速さ自体は変わりませんよね。この「間隔の変化」こそが、音の高さの変化なのです。
試験で使える公式の覚え方と計算

学生の皆さんの中には、物理のテストでドップラー効果の計算問題に頭を抱えている方もいるかもしれません。「いつプラスで、いつマイナスなのかわからない!」という悩みはとても多いです。公式は一見複雑に見えますが、実はたった一つの考え方で整理できます。
| 汎用公式 | $$f = \frac{V – v_o}{V – v_s} f_0$$ |
|---|
ここで、各文字の意味は以下の通りです。
- $f$:観測される振動数(求めたい答え)
- $f_0$:元の振動数
- $V$:音速(通常は約340m/s)
- $v_o$:観測者の速度(Observer)
- $v_s$:音源の速度(Source)
絶対に間違えない「符号」の決め方
この公式の最大の難関は、速度 $v_o$ や $v_s$ に入れるプラス・マイナスの符号です。これには、以下の鉄則ルールを適用してください。
「音源から観測者に向かう向きをプラス(+)とする」
この座標軸さえ固定してしまえば、あとは機械的に当てはめるだけです。しかし、もっと直感的に覚えたいという方には、以下の「結果から考えるテクニック」がおすすめです。
直感的!符号の決め方テクニック
数式の結果($f$)がどうなるべきかを考えます。
- 近づく場合(音が高くなるはず):分数の値を大きくしたいですよね。
→ 分子(観測者)なら足す、分母(音源)なら引く。 - 遠ざかる場合(音が低くなるはず):分数の値を小さくしたいですよね。
→ 分子(観測者)なら引く、分母(音源)なら足す。
「近づくときは音が高くなるはずだから、分数を大きくするには分母を引き算すればいいんだな」と結果から逆算して考えると、ケアレスミスを劇的に減らせますよ。
音源や観測者が動く場合の違い

少しマニアックですが、実は「音源が動く場合」と「聞く人が動く場合」では、物理的な現象の中身が少し違います。ここを理解していると、物理の理解度がグッと深まります。
音源が動くとき
これまで説明してきた救急車の例です。音源が空気を押したり引いたりするため、空気中の「波長(波の間隔)」そのものが物理的に変化しています。
聞く人(観測者)が動くとき
こちらは、静止しているスピーカーに向かって、自分が走っていくようなケースです。この場合、音源は動いていないので、空気中の波長(波の間隔)は均等のまま、変わっていません。
ではなぜ音が高く聞こえるのか?それは、観測者が自ら波に向かって突っ込んでいくことで、「波とすれ違う相対的な速度」が速くなるからです。波長は変わらないけれど、耳に飛び込んでくる波のスピードが速くなる分、たくさん波を受け取ることになり、結果として音が高く聞こえます。
「波長が変わるのか(音源移動)」、「相対速度が変わるのか(観測者移動)」というプロセスの違いはありますが、どちらも振動数が変化して聞こえるという結果は同じです。
風の影響を受ける場合の注意点

屋外での実験や応用問題では「風」の影響も無視できません。風が吹いているということは、音を伝える「空気そのもの」が流されている状態です。
例えば、音源から観測者に向かって追い風が吹いている場合、音は風に乗って通常より速く進みます。この場合、計算上の音速 $V$ は、本来の音速に風速 $w$ を足した $(V + w)$ として扱います。
逆に、向かい風の場合は音の進行が邪魔されるため、音速は $(V – w)$ となります。公式を使う際は、まず「風によってベースとなる音速が変わる」と考え、公式の中の $V$ をすべて書き換えてから計算するのがポイントです。
防災の視点でもドップラー効果をわかりやすく

さて、ここからは私の専門分野である防災の視点からドップラー効果を見ていきましょう。「音が変わる現象」というイメージが強いですが、実はこの原理は、音だけでなく光や電波にも応用され、私たちの安全を守るための最先端技術として広く活躍しているんです。
光の色が変わる赤方偏移と宇宙

ドップラー効果は音だけでなく、光(電磁波)でも起こります。音の高さが変わるように、光の場合は波長が変化すると、それは「色の変化」として現れます。
- 波長が伸びる:赤色っぽく見える(赤方偏移)
- 波長が縮む:青色っぽく見える(青方偏移)
私たちから猛スピードで遠ざかる星からの光は、波長が引き伸ばされて「赤っぽい色」に見えます。これを赤方偏移(せきほうへんい)と呼びます。かつて天文学者のエドウィン・ハッブルは、遠くの銀河ほどこの「赤方偏移」が大きい、つまり猛スピードで遠ざかっていることを発見しました。
「すべての銀河が私たちから遠ざかっている=宇宙自体が風船のように膨らんでいる」というビッグバン理論は、実はこの光のドップラー効果の観測から導き出されたものなのです。
気象レーダーでの観測や活用事例

防災士として皆さんに最も知っていただきたいのが、気象観測における「ドップラーレーダー」の活躍です。皆さんが普段、天気予報やスマホアプリで見ている「雨雲の動き」や「今後の雨の予想」、あれはこの技術のおかげで分かっていることが多いのです。
雨雲の「動き」を立体的に捉える
通常の気象レーダーは、電波を発射して雨粒に当たり、跳ね返ってくるまでの時間で「雨雲の位置」を知ります。しかし、ドップラーレーダーはさらに一歩進んでいます。
雨粒がレーダーに近づいているか、遠ざかっているかによって、戻ってくる電波の周波数がわずかに変化(ドップラー効果)します。このズレを精密に解析することで、雨雲が「どの方向に、どれくらいの速さで動いているか」だけでなく、「雲の中で風が渦を巻いているかどうか」まで分かるのです。
これにより、以前は予測が難しかった突発的な豪雨や、積乱雲の中で発生する「メソサイクロン(竜巻の親となる渦)」の予兆をいち早くキャッチできるようになりました。
気象庁では、全国に設置した気象ドップラーレーダーを用いて、詳細な降水域の分布や風の分布を観測しています。これにより、台風や集中豪雨の監視精度が飛躍的に向上しました。
(出典:気象庁『気象レーダー』)
特に最近増えているゲリラ豪雨への備えとして、レーダー情報の確認は欠かせません。スマホで雨雲レーダーを見るときは、「この裏側でドップラー効果が計算されているんだな」と思い出してみてください。
ゲリラ豪雨の仕組みや備えについては、こちらの記事でも詳しく解説しています。
医療現場で使われる検査技術

病院でもドップラー効果は命を救う技術として定着しています。特に、妊婦健診のエコー検査や、心臓の検査などで使われる「超音波ドプラ法」が有名です。
仕組みは気象レーダーと似ています。体外からプローブ(探知機)で超音波を当て、血管の中を流れる「赤血球」からの反射波を調べます。
- プローブに近づく血流:反射音が高くなる
- プローブから遠ざかる血流:反射音が低くなる
この周波数の変化を計算し、画面上で「近づく血流を赤、遠ざかる血流を青」といったように色分けして表示します(カラードップラー)。これにより、血液の流れる速さはもちろん、心臓の弁から血液が逆流していないか、血管が詰まっていないかなどを、体を切ったり傷つけたりすることなく診断できるのです。
スピードガンなど身近な利用例

もっと身近なところでは、野球の球速測定や、警察のスピード違反取締りで使われる「スピードガン」も、ドップラー効果の原理そのものです。
スピードガンからボールや走っている車に向かって電波を飛ばし、対象物に当たって反射して戻ってくる波をキャッチします。対象物の速度が速ければ速いほど、周波数のズレ(ドップラーシフト)が大きくなります。このズレの量を回路で瞬時に計算し、「150km/h」といった速度を表示しているのです。
少し詳しい話:ダブルドップラー効果
スピードガンの場合、①ガンから出た波を車が受け取る(1回目)、②車が反射してガンに波を返す(2回目)、という往復の過程を経るため、ドップラー効果が2回発生します。そのため、周波数の変化量は通常の約2倍になります。
コウモリが使うエコーロケーション

最後は自然界のハイテク技術者、コウモリの話です。コウモリは暗闇の中で超音波を出し、獲物である虫からの反射音を聞いて狩りをします。これを「エコーロケーション(反響定位)」と呼びます。
コウモリは単に「反射までの時間」で距離を測っているだけではありません。ドップラー効果による音程の変化を聞き分けることで、「その虫が自分から逃げているのか、向かってきているのか」や、さらには「虫が羽ばたくスピード」まで感知していると言われています。
コウモリは、自分が高速で飛びながら、対象の動きに合わせて発する超音波の周波数を微調整するという、とてつもなく高度な制御を行っています。現代のレーダー技術も、実はこのコウモリの能力から多くのヒントを得ているのです。
ドップラー効果をわかりやすく総まとめ

今回は、救急車のサイレンという身近な現象から、宇宙の膨張、そして最新の防災技術まで、ドップラー効果について幅広く解説してきました。
「物理の法則」と聞くと、なんだか冷たくて難しい数式だけの世界のように感じるかもしれません。しかし、その本質は「波が詰まるか、伸びるか」というとてもシンプルなものです。そしてそのシンプルな原理が、病院での診断や、豪雨から身を守るためのレーダー技術として、私たちの毎日の安全を支えてくれています。
次に街中で救急車の音を聞いたり、天気予報で「ドップラーレーダー」という言葉を耳にしたりしたときは、ぜひ今日の話を思い出してみてください。「あ、今、波が縮んでるな」「この技術が雨雲を見張ってくれているんだな」と感じることで、世界が少しだけ面白く、そして頼もしく見えるはずです。正しい知識は、いざという時にあなたと大切な人を守る、見えない「お守り」になります。









